Home

[Return to Index]

VII. Score Matching

It turns out the diffusion model we've been studying can be intepreted as a score matching model. Even though it's motivated by a different line of reasoning, we'll see that the training procedure exactly matches quantities we've seen so far. (There are connections at inference time too, but we'll cover those on the subsequent page).

We begin by abandoning the graphical model we've been studying up to now. Instead consider the general case of learning a model of observations \(\mathbf{x}\) drawn from \(p_\mathrm{data}(\mathbf{x})\).

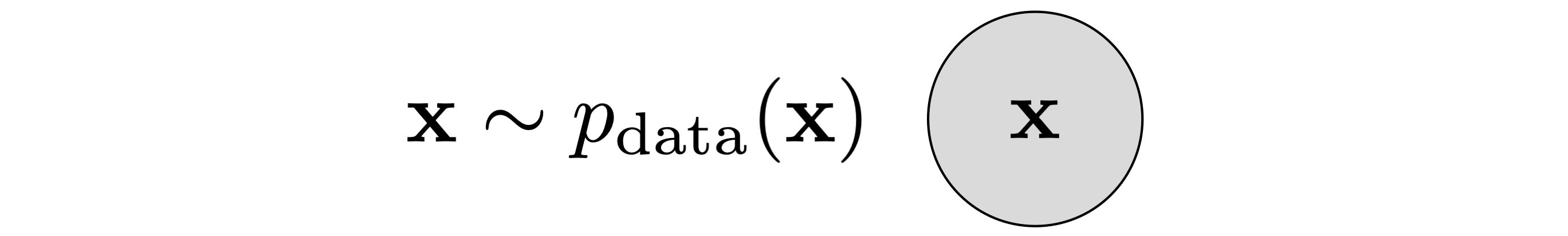
The idea behind score matching is to learn a generative model of \(p(\mathbf{x})\) by learning a network to approximate the score. (Presentation here follows Song and Ermon 2019 and Vincent 2011.)

Fundamentals

Explicit Score Matching

We'll want to approximate using a neural network \(s_\theta(\mathbf{x})\), \[ \begin{equation*} s_\theta(\mathbf{x}) \approx \nabla_{\mathbf{x}}\log p_\mathrm{data}(\mathbf{x}). \end{equation*} \] Explicit score matching can theoretically be learned by minimizing the objective \[ \begin{equation*} J(\theta) = \mathbb{E}_{\mathbf{x}\sim p_\mathrm{data}(\mathbf{x})}\|s_\theta(\mathbf{x}) - \underbrace{\nabla_{\mathbf{x}}\log p_\mathrm{data}(\mathbf{x})}_\text{hard to estimate}\|^2. \end{equation*} \] But this is intractable because we have no way to estimate the score given observations \(\{\mathbf{x}^{(i)}\}_{i=1}^N\).

De-noising Score Matching

Instead our approach will be to construct \(q_\sigma(\tilde{\mathbf{x}})\), an approximation of \(p_\mathrm{data}(\mathbf{x})\) using a non-parametric estimate. Then apply explicit score matching to \(q_\sigma(\tilde{\mathbf{x}})\).

Define. The Parzen window approximation is defined \(q_\sigma(\tilde{\mathbf{x}})\), parameterized by scalar \(\sigma > 0\). \[ \begin{align*} q_\sigma(\tilde{\mathbf{x}}) & = \mathbb{E}_{\mathbf{x}\sim p_\mathrm{data}(\mathbf{x})}[q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})]\\ q_\sigma(\tilde{\mathbf{x}}|\mathbf{x}) & = N(\mathbf{x},\sigma^2\mathbf{I}). \end{align*} \] In other words, it's a kernel density estimate over observations, with Gaussian kernels of variance \(\sigma^2\).

It turns out explicit score matching on this distribution is tractable as we will next prove.

Result. De-noising score matching can be learned by minimizing the following objective. \[ \begin{align*} J(\theta) & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\|s_\theta(\tilde{\mathbf{x}}) - \nabla_{\tilde{\mathbf{x}}}\log q_\sigma(\tilde{\mathbf{x}})\|^2\\ & \propto \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2 -2s_\theta(\tilde{\mathbf{x}}) ^\top \nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}})\right]\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\int_{\tilde{\mathbf{x}}}q_\sigma(\tilde{\mathbf{x}}) s_\theta(\tilde{\mathbf{x}}) ^\top \nabla_{\tilde{\mathbf{x}}} \log q_\sigma(\tilde{\mathbf{x}})d\tilde{\mathbf{x}}\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\int_{\tilde{\mathbf{x}}}q_\sigma(\tilde{\mathbf{x}}) s_\theta(\tilde{\mathbf{x}}) ^\top \frac{\nabla_{\tilde{\mathbf{x}}} q_\sigma(\tilde{\mathbf{x}})}{q_\sigma(\tilde{\mathbf{x}})}d\tilde{\mathbf{x}}\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\int_{\tilde{\mathbf{x}}} s_\theta(\tilde{\mathbf{x}}) ^\top \nabla_{\tilde{\mathbf{x}}} q_\sigma(\tilde{\mathbf{x}})d\tilde{\mathbf{x}}\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\int_{\tilde{\mathbf{x}}} s_\theta(\tilde{\mathbf{x}}) ^\top \nabla_{\tilde{\mathbf{x}}} \int_{\mathbf{x}}p_\mathrm{data}(\mathbf{x})q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})d\mathbf{x}d\tilde{\mathbf{x}}\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\int_{\tilde{\mathbf{x}}} s_\theta(\tilde{\mathbf{x}}) ^\top \int_{\mathbf{x}}p_\mathrm{data}(\mathbf{x})\nabla_{\tilde{\mathbf{x}}}q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})d\mathbf{x}d\tilde{\mathbf{x}}\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\int_{\tilde{\mathbf{x}}} s_\theta(\tilde{\mathbf{x}}) ^\top \int_{\mathbf{x}}p_\mathrm{data}(\mathbf{x})q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})\nabla_{\tilde{\mathbf{x}}}\log q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})d\mathbf{x}d\tilde{\mathbf{x}}\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\int_{\tilde{\mathbf{x}}} \int_\mathbf{x}p_\mathrm{data}(\mathbf{x})q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})s_\theta(\tilde{\mathbf{x}}) ^\top \nabla_{\tilde{\mathbf{x}}}\log q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})d\mathbf{x}d\tilde{\mathbf{x}}\\ & = \mathbb{E}_{\tilde{\mathbf{x}}\sim q_\sigma(\tilde{\mathbf{x}})}\left[\|s_\theta(\tilde{\mathbf{x}})\|^2\right] -2\mathbb{E}_{\mathbf{x}, \tilde{\mathbf{x}}\sim q_\sigma(\mathbf{x}, \tilde{\mathbf{x}})}\left[s_\theta(\tilde{\mathbf{x}}) ^\top \nabla_{\tilde{\mathbf{x}}}\log q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})\right]\\ & \propto \mathbb{E}_{\mathbf{x}, \tilde{\mathbf{x}}\sim q_\sigma(\mathbf{x}, \tilde{\mathbf{x}})}\| s_\theta(\tilde{\mathbf{x}}) -\underbrace{\nabla_{\tilde{\mathbf{x}}}\log q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})}_\text{tractable to estimate}\|^2 \end{align*} \] On the second line we ignore irrelevant constants. On the fourth line we apply the log-derivative trick. On the sixth line we substitute the definition of \(q_\sigma(\tilde{\mathbf{x}})\). On the eighth line we apply the log-derivative trick (in opposite direction). On the eleventh line we again ignore irrelevant constants.

Result. Specifically, we have the following estimate of the score of the Parzen window approximation. \[ \begin{align*} \log q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})& = -\frac{1}{2\sigma^2}\|\tilde{\mathbf{x}}-\mathbf{x}\|^2 + (\dots)\\ \nabla_{\tilde{\mathbf{x}}}\log q_\sigma(\tilde{\mathbf{x}}|\mathbf{x})& = \frac{1}{\sigma^2}(\mathbf{x}-\tilde{\mathbf{x}}) \approx s_\theta(\tilde{\mathbf{x}}) \end{align*} \] This is what gives us the "de-noising" interpretation; because the neural network is trying to approximate the amount of noise that is added to clean observations \(\mathbf{x}\) to produce \(\tilde{\mathbf{x}}\).

Remark. Because \(p_\mathrm{data}(\mathbf{x}) \neq q_\sigma(\tilde{\mathbf{x}})\) we have no guarantee that learning a generative model of \(q_\sigma(\tilde{\mathbf{x}})\) can recover \(p_\mathrm{data}(\mathbf{x})\). Our work relies on the fact that when \(\sigma\approx 0, p_\mathrm{data}(\mathbf{x}) \approx q_\sigma(\tilde{\mathbf{x}})\).

Sampling and Training via Annealed Langevin Dynamics

Song and Ermon 2019 propose sampling using Langevin dynamics, which is an MCMC method that can draw samples from a distribution given queries of the score.

Specifically, they use the following update rule \[ \begin{align*} \mathbf{x}_{t+1} = \mathbf{x}_t + \frac{1}{2}\eta_t s_\theta(\mathbf{x}_t) + \sqrt{\eta_t}\ \mathbf{z}_t, \quad \quad \mathbf{z}_t\sim N(\mathbf{0},\mathbf{I}) \end{align*} \]

which produces a valid sample as long as \(\eta_t \rightarrow 0\).

However, one concern is that using a fixed level \(\sigma\) leads to much of the input space unexplored at training time. Instead, the authors propose annealed Langevin dynamics where we train a single score network \(s_\theta(\mathbf{x})\) which can handle a variety of discrete noise scales.

Let the noise scales \(\{\sigma_i\}_{i=1}^T\) satisfy a decreasing geometric sequence such that \(\frac{\sigma_1}{\sigma_2} = \dots = \frac{\sigma_{T-1}}{\sigma_T}\).

We define the following loss weight for training time, and add an annealing factor to \(\eta_t\) at inference time. \[ \begin{align*} J(\theta, \sigma_t) & = \underbrace{\sigma_t^2}_\text{loss weight}\mathbb{E}_{\mathbf{x}, \tilde{\mathbf{x}}\sim q_{\sigma_t}(\mathbf{x}, \tilde{\mathbf{x}})}\| s_\theta(\tilde{\mathbf{x}}) -\nabla_{\tilde{\mathbf{x}}}\log q_{\sigma_t}(\tilde{\mathbf{x}}|\mathbf{x})\|^2 \tag{training time}\\ & = \mathbb{E}_{\mathbf{x}, \tilde{\mathbf{x}}\sim q_{\sigma_t}(\mathbf{x}, \tilde{\mathbf{x}})}\left\| \sigma_t s_\theta(\tilde{\mathbf{x}}) -\frac{\mathbf{x}-\tilde{\mathbf{x}}}{\sigma_t}\right\|^2\\ \eta_t & = \eta\frac{\sigma_t^2}{\sigma_T^2}. \tag{inference time} \end{align*} \] These choices ensure that:

Diffusion Models as Score Matching Models

We'll now re-adopt the notation we've used on previous pages. Specifically, we draw Monte Carlo samples \[ \begin{align*} \mathbf{x}_t & = \alpha_t \mathbf{x}_0 + \sigma_t\boldsymbol\epsilon_t. \end{align*} \] Result. The training objective for a diffusion model can be interpreted as score matching on \(\bar{\mathbf{x}}_t\) with noise scales \(\lambda_t\), defined \[ \begin{align*} \bar{\mathbf{x}}_t \triangleq \frac{\mathbf{x}_t}{\alpha_t}\quad\quad\lambda_t \triangleq \frac{\sigma_t}{\alpha_t}. \end{align*} \] Specifically, a score matching model with these definitions is equivalent to diffusion where we

  1. Use the \(\boldsymbol\epsilon\)-prediction simple loss (i.e. a weighted ELBO).
  2. Parameterize the network to predict \(-\boldsymbol\epsilon_t / \lambda_t\) (a scalar multiple of \(\boldsymbol\epsilon\) prediction).
  3. Parameterize the input to the network as \(\mathbf{x}_t/\alpha_t\) (a scalar multiple of \(\mathbf{x}_t\)).

An important caveat is that the distribution over \(\{\alpha_t,\sigma_t\}\) or, equivalently, \(\{\lambda_t\}\) which controls the Monte Carlo samples will be slightly different. This comes down to differences in the noise schedule, which we'll remark on after the proof.

Proof.

It's easy to see that the Monte Carlo samples in the diffusion setup \(\tilde{\mathbf{x}}_t\) are equivalent to scaling by \(\alpha_t\) and adding Gaussian noise with scale \(\lambda_t\). \[ \begin{align*} \tilde{\mathbf{x}}_t &= \alpha_t \mathbf{x}_0 + \sigma_t\boldsymbol\epsilon_t\\ \frac{\tilde{\mathbf{x}}_t}{\alpha_t} & = \mathbf{x}_0 + \frac{\sigma_t}{\alpha_t}\boldsymbol\epsilon_t \tag{divide both sides}\\ \bar{\mathbf{x}}_t & = \mathbf{x}_0 + \lambda_t \boldsymbol\epsilon_t \tag{from definitions above}. \end{align*} \]

Next consider the network parameterization. With \(\boldsymbol\epsilon\)-prediction, we try to learn \[ \begin{align*} g_\theta(\bar{\mathbf{x}}_t) & \approx \boldsymbol\epsilon_t = \frac{1}{\lambda_t}(\bar{\mathbf{x}}_t - \mathbf{x}_0). \end{align*} \] Meanwhile, in score matching we try to learn \[ \begin{align*} s_\theta(\bar{\mathbf{x}}_t) & \approx \nabla_{\bar{\mathbf{x}}_t} \log q_{\lambda_t}(\bar{\mathbf{x}}_t|\mathbf{x}_0) = \frac{1}{\lambda_t^2}(\mathbf{x}_0 - \bar{\mathbf{x}}_t) = -\frac{1}{\lambda_t}\boldsymbol\epsilon_t. \end{align*} \] Therefore the score matching network target is equivalent to the \(\boldsymbol\epsilon\) prediction target, scaled by a timestep-dependent constant \(-\lambda_t\).

Finally, the score matching loss function can be converted to the familiar \(\boldsymbol\epsilon\) prediction simple loss as follows. \[ \begin{align*} J(\theta, \lambda_t) & = \lambda_t^2\|s_\theta(\bar{\mathbf{x}}_t) - \nabla_{\bar{\mathbf{x}}_t} \log q(\bar{\mathbf{x}}_t|\mathbf{x}_0)\|^2\\ & = \lambda_t^2\left\|\frac{\boldsymbol\epsilon_t}{\lambda_t} - \frac{\hat{\boldsymbol\epsilon_t}}{\lambda_t}\right\|^2\\ & = \|\hat{\boldsymbol\epsilon}_t - \boldsymbol\epsilon_t\|^2. \end{align*} \] This concludes the proof.

Remark. We'll make the connection to inference time in the subsequent page on the SDE extension to the score matching framework.

Remark. This provides yet another interpretation of the noise schedule, via \(\lambda_t=\frac{\sigma_t}{\alpha_t} = \mathrm{SNR}_t^{-\frac{1}{2}}\).

The cosine schedule we've been familiar with straightforwardly implies a set of choices for \(\lambda_t\). Meanwhile, the score matching setup trains with a geometric sequence, implying \(\lambda_t\) is linearly spaced in \(\log \mathrm{SNR}_t\).

Below, we plot the difference between these two schedules fixing \(T=15\) discrete noise scales [Footnote 1]. The interpretation is that at training time, we pick uniformly at random from the set of \(\log \lambda_t\) below to construct our Monte Carlo samples \(\bar{\mathbf{x}}_t\). Meanwhile, at inference time we iterate over the same steps, from right to left, to de-noise an input.

[Footnote 1] For the score matching setup, we use a range over \(\lambda_\text{min} = 0.002\) to \(\lambda_\text{max} = 80\), which are hyper-parameters specified in Karras et al. 2022.